AtomAlpaca
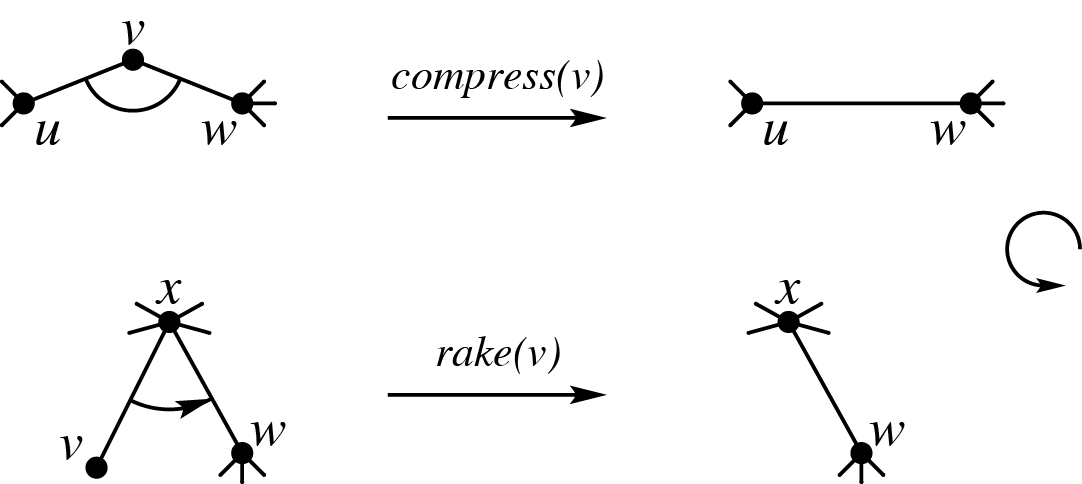
给你一棵树,边上有信息,提供两种合并方式(其实就是 Top Tree 那套理论里的 compress 和 rake)。

合并两个信息需要通过调用交互库来实现。你可以用不超过 次操作进行预处理,每次不超过 次操作回答节点 的 -邻域信息并。
考虑建一棵静态 Top Tree 出来。
一个建法是对原树进行树剖,然后考虑每一条重链,对于这条重链上的每一个点,递归处理所有轻儿子把它们的子树缩成一个簇,然后对这些轻儿子簇和这一个节点和它重儿子连成的边形成的那一个簇进行合并。
大概过程就是类似全局平衡二叉树,对于这一排簇,每次以簇的大小为权值找到带权中点,然后把两边分别递归处理,然后再用 合并起来。
这样我们就把一个点所有轻儿子的簇 到了重儿子那个簇上。然后我们每条重链就只剩下一条链了,这时我们再重复上述步骤把它分治地 成一个簇即可。
然后对于三个簇 ,如果 是 或者 来的,那么我们就把 和 连边,这样形成的就是一棵 Top Tree,并且我们能保证这棵树的树高是 的。
我们令 为一个簇的两个端点的距离, 是簇的直径。然后规定每个簇两个顶点有“上下”之分,两个簇能 当且仅当它们的上界点相同,能 当且仅当一个簇的下界点和另一个的上界点相同。可以结合上面的图和题面理解这个约定。
然后我们考虑维护 是树簇 的上/下界点在该树簇内的 -邻域的信息, 是树簇 的上/下界点在该树簇外的 -邻域的信息。维护的时候我们对这个簇是 还是 得到的进行讨论。当这个点是 得到的时,有:
否则
具体式子怎么推出来的,其实在上面的图上把式子代表的范围圈出来就能感性地看出来要合并哪些信息了。举个例子:
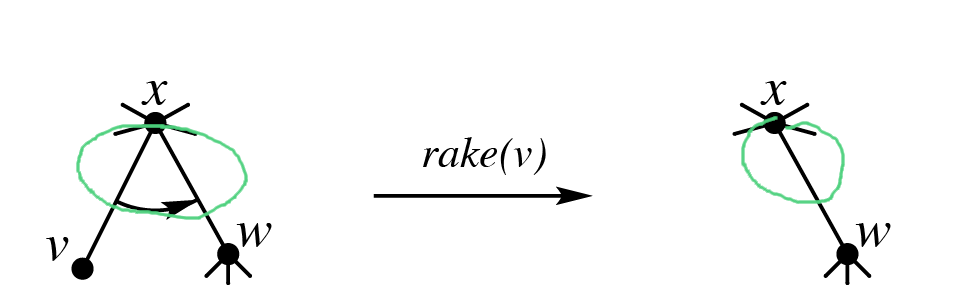
比如芝士 ,不难发现就是 和 并起来。
然后 是依赖儿子的,而 是依赖父亲和 的,所有需要分两次求。
考虑我们怎么进行查询。首先我们找到包含这个点的一个最小簇,然后不断往上跳直到最后一个的直径小于 的簇。由于树高是 的所以复杂度是有保证的。
这时我们的答案分为了簇内的所有信息,和两个簇端点外面一段距离的信息的并。形式化地说是 这样。
但是这样每次查询我们都需要进行两次合并,这是过不了最后一个测试点的。然后我们发现查询答案的时候 这两个信息一定会被合并,所有我们可以提前把所有的后者和合并到前者上,从而将合并次数减少到一次。
然后为了减少操作次数,如果合并的信息两者中有 就直接返回另一个元素;对于每个簇的信息我们第三维只维护到簇的直径。
#include <bits/stdc++.h>
#include "count.h"
typedef info I;
const int MAX = 5e5 + 5;
const int RAKE = 1;
int n, cnt, top, rt, tot;
int h[MAX], st[MAX], dep[MAX], fa[MAX], _fa[MAX], siz[MAX], sz[MAX], son[MAX], U[MAX], V[MAX], ls[MAX], rs[MAX], ln[MAX], typ[MAX], lm[MAX], rm[MAX], mx[MAX];
int fth[MAX][25];
std::vector <I> f[MAX][2], g[MAX][2];
struct E { int v, x; } e[MAX << 2];
void add(int u, int v) { e[++tot] = {v, h[u]}; h[u] = tot; }
inline I R(I a, I b)
{
if (isempty(a)) { return b; }
if (isempty(b)) { return a; }
return MR(a, b);
}
inline I C(I a, I b)
{
if (isempty(a)) { return b; }
if (isempty(b)) { return a; }
return MC(a, b);
}
inline int lca(int u, int v)
{
if (dep[u] < dep[v]) { std::swap(u, v); }
for (int i = 20; i >= 0; --i) { if (dep[fth[u][i]] >= dep[v]) { u = fth[u][i]; } }
if (u == v) { return u; }
for (int i = 20; i >= 0; --i) { if (fth[u][i] != fth[v][i]) { u = fth[u][i]; v = fth[v][i]; } }
return fth[u][0];
}
inline int dis(int u, int v) { return dep[u] + dep[v] - 2 * dep[lca(u, v)]; }
inline I F(int u, int t, int k)
{
if (k < 0) { return emptyinfo; }
if (k >= f[u][t].size()) { return f[u][t].back(); }
return f[u][t][k];
}
inline I G(int u, int t, int k)
{
if (k < 0) { return emptyinfo; }
if (k >= g[u][t].size()) { return g[u][t].back(); }
return g[u][t][k];
}
void dfs0(int u)
{
siz[u] = 1; dep[u] = dep[fa[u]] + 1; fth[u][0] = fa[u];
for (int i = 1; i <= 20; ++i) { fth[u][i] = fth[fth[u][i - 1]][i - 1]; }
for (int i = h[u]; i; i = e[i].x)
{
int v = e[i].v; dfs0(v);
if (siz[v] > siz[son[u]]) { son[u] = v; } siz[u] += siz[v];
}
}
void initf(int u)
{
_fa[ls[u]] = _fa[rs[u]] = u; sz[u] = sz[ls[u]] + sz[rs[u]];
if (typ[u] == RAKE)
{
mx[u] = std::max(lm[ls[u]] + lm[rs[u]], std::max(mx[ls[u]], mx[rs[u]]));
lm[u] = std::max(lm[ls[u]], lm[rs[u]]);
rm[u] = std::max(rm[ls[u]], ln[ls[u]] + lm[rs[u]]);
ln[u] = ln[ls[u]]; U[u] = U[ls[u]]; V[u] = V[ls[u]];
f[u][0].resize(mx[u] + 1); f[u][1].resize(mx[u] + 1);
for (int i = 0; i <= mx[u]; ++i)
{
f[u][0][i] = R(F(ls[u], 0, i), F(rs[u], 0, i));
f[u][1][i] = R(F(ls[u], 1, i), F(rs[u], 0, i - ln[u]));
}
}
else
{
mx[u] = std::max(rm[ls[u]] + lm[rs[u]], std::max(mx[ls[u]], mx[rs[u]]));
lm[u] = std::max(lm[ls[u]], ln[ls[u]] + lm[rs[u]]);
rm[u] = std::max(rm[rs[u]], ln[rs[u]] + rm[ls[u]]);
ln[u] = ln[ls[u]] + ln[rs[u]]; U[u] = U[ls[u]]; V[u] = V[rs[u]];
f[u][0].resize(mx[u] + 1); f[u][1].resize(mx[u] + 1);
for (int i = 0; i <= mx[u]; ++i)
{
f[u][0][i] = C(F(ls[u], 0, i), F(rs[u], 0, i - ln[ls[u]]));
f[u][1][i] = C(F(ls[u], 1, i - ln[rs[u]]), F(rs[u], 1, i));
}
}
}
int build(int l, int r, int k)
{
if (l == r) { return st[l]; }
int sm = 0, p = l, u = ++cnt, now = 0; typ[u] = k;
for (int i = l; i <= r; ++i) { sm += sz[st[i]]; }
while (p < r - 1 and (now + sz[st[p]]) * 2 <= sm) { now += sz[st[p++]]; }
ls[u] = build(l, p, k); rs[u] = build(p + 1, r, k);
initf(u); return u;
}
void dfs1(int u)
{
int tp = top + 1, v = u, rt; if (u != 1) { st[++top] = u; }
for (; son[v]; v = son[v])
{
st[rt = ++top] = son[v];
for (int i = h[v]; i; i = e[i].x)
{
int k = e[i].v;
if (k != son[v]) { dfs1(k); }
}
int tmp = build(rt, top, RAKE);
st[top = rt] = tmp;
}
int tmp = build(tp, top, 0); st[top = tp] = tmp;
}
void initg(int u)
{
if (typ[u] == RAKE)
{
g[ls[u]][0].resize(mx[u] + 1); g[ls[u]][1].resize(mx[u] + 1);
g[rs[u]][0].resize(mx[u] + 1); g[rs[u]][1] = {emptyinfo};
for (int i = 0; i <= mx[u]; ++i)
{
g[ls[u]][0][i] = R(F(rs[u], 0, i), G(u, 0, i));
g[ls[u]][1][i] = G(u, 1, i);
g[rs[u]][0][i] = R(C(F(ls[u], 0, i), G(ls[u], 1, i - ln[ls[u]])), G(u, 0, i));
}
}
else
{
g[ls[u]][0].resize(mx[u] + 1); g[ls[u]][1].resize(mx[u] + 1);
g[rs[u]][0].resize(mx[u] + 1); g[rs[u]][1].resize(mx[u] + 1);
for (int i = 0; i <= mx[u]; ++i)
{
g[ls[u]][0][i] = G(u, 0, i);
g[ls[u]][1][i] = C(G(u, 1, i - ln[rs[u]]), F(rs[u], 0, i));
g[rs[u]][0][i] = C(G(u, 0, i - ln[ls[u]]), F(ls[u], 1, i));
g[rs[u]][1][i] = G(u, 1, i);
}
}
}
void dfs2(int u) { if (u <= n) { return ; } initg(u); dfs2(ls[u]); dfs2(rs[u]); }
void init(int _T, int _n, int _q, std::vector<int> _fa, std::vector<info> _e, int _M)
{
cnt = n = _n;
for (int i = 0; i < n - 1; ++i)
{
fa[i + 2] = _fa[i]; add(_fa[i], i + 2);
U[i + 2] = fa[i + 2]; V[i + 2] = i + 2;
lm[i + 2] = rm[i + 2] = mx[i + 2] = ln[i + 2] = sz[i + 2] = 1;
f[i + 2][0] = f[i + 2][1] = {emptyinfo, _e[i]};
}
dfs0(1); dfs1(1);
rt = st[1]; g[rt][0] = g[rt][1] = {emptyinfo};
dfs2(rt);
for (int i = 2; i <= cnt; ++i)
{
for (I & j : g[i][0]) { j = C(j, f[i][0].back()); }
}
}
I ask(int u, int d)
{
int p = u; if (p == 1) { p = 2; }
while (mx[_fa[p]] <= d and _fa[p]) { p = _fa[p]; }
return C(G(p, 0, d - dis(u, U[p])), G(p, 1, d - dis(u, V[p])));
}