「题解」P4671 Polygon

Table of contents

• 题目
• 分析
• 代码

题目

link

分析

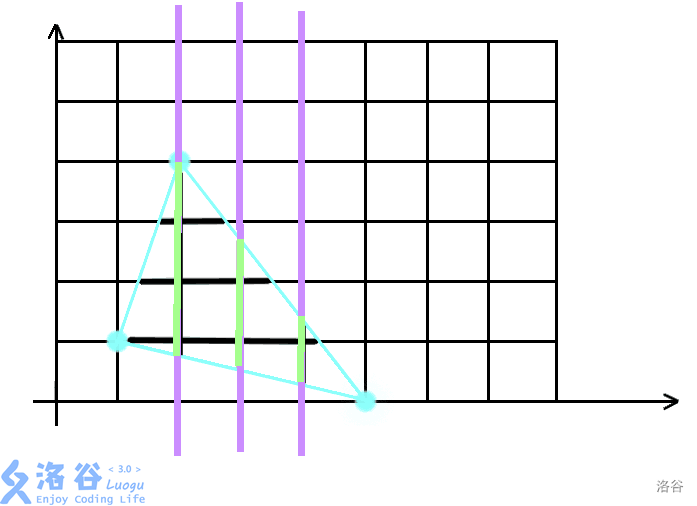
我们首先拿第一张图片举例。

将这个图形沿竖直方向的网格线划分为若干个梯形（或三角形）。根据梯形的面积公式，每个梯形的面积都是它相邻的两条截线的长度和的一半，因此整个多边形的面积就是竖直方向所有截线长度的和。横向的长度也是同样地处理。

但上述方法我们显然少考虑了一种情况。如图二：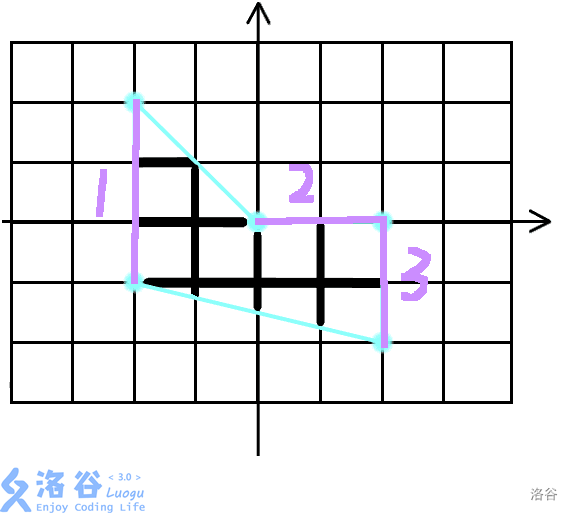

其中标为紫色的线段也属于上述计算范围内的“截线”，但是这些线段并不严格在多边形内。我们考虑去掉这部分对答案的贡献。

我们发现，这样的线段一定是且仅是多边形上与网格线重合的边，这样的边一定有一侧是多边形内侧，一侧是多边形外侧，因此划分计算面积时一定只对一个梯形(三角形)的面积产生贡献，也就是对答案造成了该线段长度的一半的贡献。因此我们只要从答案中减去这样的边的长度的一半即可。

综上，我们得到最终答案是该多边形面积的两倍减去与网格线平行的边长度和的一半。

另：题面里第一张图片并不是第一个样例的配图

代码

#include <bits/stdc++.h>

using std::cin;
using std::cout;

typedef long long ll;
const ll MAX = 1e5 + 5;
ll n, x[MAX], y[MAX], S;

int main()
{
  cin >> n;
  for (int i = 1; i <= n; ++i) { cin >> x[i] >> y[i]; }
  x[0] = x[n]; y[0] = y[n];
  for (int i = 1; i <= n; ++i) { S += (x[i] * y[i - 1]) - (x[i - 1] * y[i]); }
  double ans = std::fabs(S);
  for (int i = 1; i <= n; ++i)
  {
    if (x[i] == x[i - 1]) { ans -= std::fabs(1.0 * (y[i] - y[i - 1]) / 2.0); }
    if (y[i] == y[i - 1]) { ans -= std::fabs(1.0 * (x[i] - x[i - 1]) / 2.0); }
  }
  cout << std::fixed << std::setprecision(6) << ans;
  return 0;